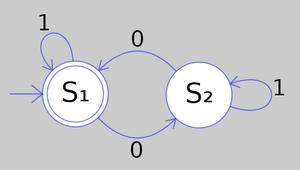
The machine operates on an infinite[4] memory tape divided into discrete cells,[5] each of which can hold a single symbol drawn from a finite set of symbols called the alphabet of the machine. It has a &quot;head&quot; that, at any point in the machine&#39;s operation, is positioned over one of these cells, and a &quot;state&quot; selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine&#39;s own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right,[6] or halts the computation. The choice of which replacement symbol to write, which direction to move the head, and whether to halt is based on a finite table that specifies what to do for each combination of the current state and the symbol that is read. Like a real computer program, it is possible for a Turing machine to go into an infinite loop which will never halt.

<ol>
<li>Whatever the hell Leibniz was thinking about</li>
<li>Information theory</li>
<li>Computability theory (Turing)</li>
<li>Cellular automata</li>
<li>Computational complexity theory</li>
<li>Fractal geometry</li>
<li>Asymmetric cryptography</li>
<li>Modern AI mechanisms</li>
<li>Programmable cryptography</li>
<li>Quantum computing</li>
</ol>